регрессия моделирование статистика mathcad

Главная задача, которая решается с помощью регрессионного анализа, - создание математических моделей некоторых объектов или явлений на основе экспериментов или наблюдений. Эти модели представляют собой определённые математические соотношения между показателями работы объекта или характеристиками наблюдаемого явления и обусловливающими их величинами. Будем называть зависимыми переменными, выходными характеристиками или откликами объекта, а - входными переменными, независимыми характеристиками или факторами. Для одного и того же объекта можно создать множество моделей:

причём каждая описывает лишь один из показателей, интересующих исследователя. В зависимости от целей исследования один и тот же объект с одинаковыми показателями может описываться различными моделями.

Выбор подходящей модели - это в значительной степени искусство, и при определении её вида часто решающую роль играют опыт и знания исследователя. Модель всегда отражает данное явление с некоторым приближением.

Есть и ещё одна причина, по которой модель не отражает протекающее явление абсолютно точно. Всегда есть величины, которые влияют на результаты, но не измеряются во время эксперимента. Часть из них имеет систематический характер и в силу этого может с течением времени вызвать изменения коэффициентов модели. Другая же часть меняется случайным образом, подчиняясь некоторому закону распределения. Такие величины ещё называют случайными возмущениями. В силу их действия повторные опыты при одних и тех же значениях факторов будут давать различные значения зависимой переменной. Модель не может точно учесть влияние случайных возмущений в каждом отдельном измерении, она показывает лишь некоторые усреднённые характеристики.

Следовательно, нет оснований говорить об "истинной" модели в полном смысле слова. Тем не менее, модели с успехом используются на практике. Обычно под "истинным" значением понимают условное математическое ожидание зависимой переменной при заданных значениях факторов:

где Е - знак математического ожидания.

Это равенство называется уравнением регрессии и показывает изменение среднего значения отклика объекта при изменениях факторов. Фактически измеряемая выходная характеристика есть

где - случайное возмущение. Чаще всего принимают, что действие на объект множества случайных возмущений эквивалентно действию одного единственного возмущения с нормальным распределением, нулевым математическим ожиданием и дисперсией. Это предположение выполняется достаточно хорошо для многих практических задач, в которых все случайные возмущения оказывают воздействия, соизмеримые одно с другим. Основанием этому служит центральная предельная теорема теории вероятностей.

Существует большое число различных регрессионных моделей, определяемых конкретным видом функции, где всегда присутствуют некоторые коэффициенты, которые надо определять по экспериментальным данным. В зависимости от того, как эти коэффициенты входят в уравнение регрессии, модели делятся на линейные и нелинейные по параметрам.

Например, модель

• - нелинейна, а
• - линейна.

Под линейной обычно понимают модель, линейную по параметрам. Например, модель

Линейна

по отношению к коэффициентам, не нелинейна по отношению к факторам.

Нередко регрессионные модели представляют полиномами по степеням факторов. Подобное представление опирается на тот факт, что отклики - часто непрерывные функции от факторов и их можно разложить в ряд Тейлора.

Ясно, что все функции, разложимые в ряд Тейлора, можно аппроксимировать полиномами. Это важно отметить, так как полиномами трудно аппроксимировать функции с разрывами, т.е. не имеющие производных. Полиномы не годятся для описания явлений со скачкообразными изменениями выходной характеристики при изменении факторов, функций с гистерезисом, релейных функций и т.п.

Когда исследуется периодический процесс, его наилучшее описание можно получить разложением в ряд Фурье:

где - частота, меняющаяся в пределах. Такие модели используются в электротехнике, геофизике, океанологии, биологии, медицине и других прикладных областях.

Для описания временных характеристик используется ещё так называемая модель распределённого лага:

Это выражение предполагает, что измерения делаются в дискретные моменты времени, отстоящие друг от друга на интервал. Через обозначена выходная характеристика в -й момент времени, т.е.

а - та же самая величина, измеренная на тактов раньше; - значение фактора, измеренное с запаздыванием на тактов по отношению к текущему i -му моменту.

В уравнении (1.1) записана одна выходная характеристика, но аналогичные модели можно строить и когда в исследовании участвует несколько откликов. Если для случайных процессов вход явно не определён, то пользуются так называемой моделью авторегрессии:

Моделью авторегрессии, например, описывается изменение числа пассажиров на железнодорожной магистрали через определённое время. Отклик может рассматриваться и как функция некоторого фактора (нескольких факторов), заданного через определённые промежутки времени:

Представление всех моделей в единой форме удобно при организации вычислительных процедур регрессионного анализа, однако, аналогия между моделями разных видов отнюдь не полная. Например, модели (1.2) и (1.3) описывают зависимость выходной характеристики в i -й момент от её значений в предыдущие моменты, а это предполагает зависимость между наблюдениями во времени, которая влечёт за собой значительные изменения как в вычислительной процедуре, так и в статистическом анализе результатов.

Многие нелинейные по параметрам модели линеаризуемы с помощью подходящего преобразования переменных. В биологии, например, используется так называемая логистическая функция, показывающая зависимость доли погибших вредных насекомых

Число погибших насекомых, - общее число насекомых при заданной дозе инсектицида. Логистическая зависимость имеет вид

и говорит о том, что очень маленькие и очень большие дозы яда не приводят к существенному изменению доли погибших насекомых (при очень малых дозах гибнут самые не жизнестойкие, а при очень больших - все).

Если к логистической зависимости применить преобразование

то, как легко проверить, она примет вид

а эта зависимость линейна относительно искомых параметров.

В моделях, которые рассматривались до сих пор, предполагалось, что все независимые переменные могут меняться в заданных интервалах непрерывно. Однако в некоторых задачах часть факторов имеет качественный характер и может принимать только определённые дискретные значения. В этом случае в модель вводят так называемые индикаторные переменные, показывающие, имел ли некоторый фактор в определённом наблюдении заданное значение или нет. Фактор с качественными уровнями можно представить индикаторными переменными, принимающими только значения 0 и 1.

Примером послужит задача построения модели количества газовых пор в сварном шве при аргонодуговой сварке никеля в зависимости от состава покрытия электрода (криолит - , титан - , алюминий -, фтористый натрий -), а также от условий сварки - времени горения - и длины дуги - Длина дуги - качественный фактор, который может принимать только два значения: длинная дуга () и короткая дуга. Линейная по параметрам и факторам модель имеет вид:

причём переменная равна 1 в экспериментах с длинной дугой и 0 - с короткой.

Другой пример индикаторной переменной даёт исследование выхода химической реакции в зависимости от температуры (), давления () и pH раствора (). Опыты проводятся с сырьём, поставляемым фирмами А, В и С. Фирму-поставщик можно рассматривать как фактор с качественными уровнями, принимающими значения. Его влияние можно представить двумя индикаторными переменными и. Вот линейная по параметрам и факторам модель для этого случая:

Если используется сырьё фирмы А, то в этом уравнении полагаем =1, =0, для сырья фирмы В - =0, =1, а для фирмы С - =0 и =0.

В данном случае нельзя было бы выбрать для фирмы С отдельную индикаторную переменную (), поскольку такой выбор всегда приводил бы к равенству

а это - линейная зависимость между переменными, наличие которой приводит к серьёзным вычислительным трудностям.

Индикаторные переменные могут участвовать и в более сложных моделях. Если, например, предполагается, что действие факторов (температура, давление, pH раствора на выход у) зависит и от взаимного влияния между факторами, модель может принять вид:

Могут использоваться и некоторые другие модели. Одни удобнее при описании данных наблюдения определённых явлений, другие дают известные преимущества при обработке данных.

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Размещено на http://www.allbest.ru/

• Задача
• Расчет параметров модели
• Список литературы

Задача

По десяти кредитным учреждениям получены данные, характеризующие зависимость объема прибыли (Y) от среднегодовой ставки по кредитам (X 1), ставки по депозитам (X 2) и размера внутрибанковских расходов (X 3).

Требуется:

1. Осуществить выбор факторных признаков для построения двухфакторной регрессионной модели.

2. Рассчитать параметры модели.

3. Для характеристики модели определить:

Ш линейный коэффициент множественной корреляции,

Ш коэффициент детерминации,

Ш средние коэффициенты эластичности, бетта-, дельта- коэффициенты.

Дать их интерпретацию.

4. Осуществить оценку надежности уравнения регрессии.

5. Оценить с помощью t-критерия Стьюдента статистическую значимость коэффициентов уравнения множественной регрессии.

6. Построить точечный и интервальный прогнозы результирующего показателя.

7. Отразить результаты расчетов на графике.

1. Выбор факторных признаков для построения двухфакторной регрессионной модели

Линейная модель множественной регрессии имеет вид:

Y i = 0 + 1 x i 1 + 2 x i 2 + … + m x im + i

регрессионная модель детерминация корреляция

Коэффициент регрессии j показывает, на какую величину в среднем изменится результативный признак Y, если переменную x j увеличить на единицу измерения.

Статистические данные для 10 исследуемых кредитных учреждений по всем переменным даны в таблице 2.1 В этом примере n = 10, m = 3.

Таблица 2.1

Х 2 - ставка по депозитам;

Х 3 - размер внутрибанковских расходов.

Чтобы убедиться в том, что выбор объясняющих переменных оправдан, оценим связь между признаками количественно. Для этого вычислим матрицу корреляций (расчет проведен в Excel Сервис - Анализ данных - Корреляция). Результаты вычислений представлены в таблице 2.2.

Таблица 2.2

Проанализировав данные можно сделать вывод что на объем прибыли Y имеют влияние такие фактории как: среднегодовая ставка по кредитам Х 1 , ставка по депозитам Х 2 и размер внутрибанковских расходов Х3. Самую тесную корреляционную связь с переменной имеет Х 1 - среднегодовая ставка по кредитам (r yx 1 =0,925). В качестве второй переменной для построения модели выбираем меньшую величину коэффициента корреляции для избежания мультиколлинеарности. Мультиколлинеарность - это линейная, или близкая к ней связь между факторами. Таким образом при сравнении Х 2 и Х 3 ми выбираем Х 2 - ставка по депозитам так как она составляэт 0,705 что на 0,088 меньше чем Х 3 - размер внутрибанковских расходов которое составило 0,793.

Расчет параметров модели

Строим эконометрическую модель:

Y= f (Х 1 , Х 2 )

где Y - объем прибыли (зависимая переменная)

Х 1 - среднегодовая ставка по кредитам;

Х 2 - ставка по депозитам;

Оценка параметров регрессии осуществляется по методу наименьших квадратов, используя данные, приведенные в таблице 2.3

Таблица 2.3

Анализ уравнения множественной регрессии и методика определения параметров становятся более наглядными, если воспользоваться матричной формой записи уравнения

где Y - вектор зависимой переменной размерности 101, представляющий собой значение наблюдений Y i ;

Х - матрица наблюдений независимых переменных Х 1 и Х 2 , размерность матрицы равна 103;

Подлежащий оцениванию вектор неизвестных параметров размерности 31;

Вектор случайных отклонений размерности 101.

Формула для вычисления параметров регрессионного уравнения:

А= (Х Т Х) - 1 Х Т Y

Для операций с матрицами использовались следующие функции Excel:

ТРАНСП (массив ) для транспонирования матрицы Х. Транспонированной называется матрица Х Т, в которой столбцы исходной матрицы Х заменяются строками с соответствующими номерами;

МОБР (массив ) для нахождения обратной матрицы;

МУМНОЖ (массив1, массив 2), которая вычисляет произведение матриц. Здесь массив 1 и массив 2 перемножаемые массивы. При этом количество столбцов аргумента массив 1 должно быть таким же, как количество строк аргумента массив 2. Результатом является массив с таким же числом строк, как массив 1 и таким же числом столбцов, как массив 2.

Результаты вычислений, проведенные в Excel:

Уравнение зависимости объема прибыли от среднегодовой ставки по кредитам и ставки по депозитам можно записать в следующем виде:

у = 33,295 + 0,767х 1 + 0,017х 2

Модель линейной регрессии, в которой вместо истинных значений параметров подставлены их оценки, имеет вид:

Y=Х+е = Y+е

где Y - оценка значений Y, равная Х;

е - остатки регрессии.

Расчетные значения Y определяются путем последовательной подстановки в эту модель значений факторов, взятых для каждого наблюдения.

Прибыль зависит от среднегодовой ставки по кредитам и ставки по депозитам. То есть с увеличением ставки по депозитам на 1000 рублей приводит к увеличению прибыли на 1,7 рублей, при неизменной величине ставки по депозитам, а увеличение ставки депозитов в 2 раза приведет к увеличению прибыли в 1,534 раза при прочих неизменных условиях.

Характеристики регрессионной модели

Промежуточные вычисления представлены в таблице 2.4.

Таблица 2.4

			(y i -) 2	(y i -) 2	е t			(е t -е t-1 ) 2	(x i 1 -) 2	(x i 2 -) 2

Результаты регрессионного анализа содержатся в таблицах 2.5 - 2.7.

Таблица 2.5.

	Наименование		Результат
	Коэффициент множественной корреляции
	Коэффициент детерминации R 2
	Скорректированный R 2
	Стандартная ошибка
	Наблюдения

Таблица 2.6

Таблица 2.7

	Коэффициенты	Стандартная ошибка	t-статистика

В третьем столбце содержатся стандартные ошибки коэффициентов регрессии, а в четвертом t-статистика, используемая для проверки значимости коэффициентов уравнения регрессии.

а) Оценка линейного коэффициента множественной корреляции

б) Коэффициент детерминации R 2

Коэффициент детерминации показывает долю вариации результативного признака под воздействием изучаемых факторов. Следовательно, 85,5% вариации зависимой переменной учтено в модели и обусловлено влиянием включенных факторов.

Скорректированный R 2

в) Средние коэффициенты эластичности, бета-, дельта - коэффициенты

Учитывая, что коэффициент регрессии невозможно использовать для непосредственной оценки влияния факторов на зависимую переменную из-за различия единиц измерения, используем коэффициент эластичности (Э) и бета-коэффициент , которые рассчитываются по формулам:

Коэффициент эластичности показывает, на сколько процентов изменяется зависимая переменная при изменении фактора на 1 процент.

При увеличении среднегодовой ставки по кредитам на 1%, объем прибыли увеличится в среднем на 0,474%. При увеличении ставки по депозитам на 1%, объем прибыли увеличится в среднем на 0,041%.

где - среднестатистическое отклонение фактора j.

значение (x i 1 -) 2 =2742,4 табл. 2.4 столбец 10;

значение (x i 2 -) 2 =1113,6 табл. 2.4 столбец 11;

Бета-коэффициент, с математической точки зрения, показывает, на какую часть величины среднего квадратического отклонения меняется среднее значение зависимой переменной с изменением независимой переменной на одно среднеквадратическое отклонение при фиксированном на постоянном уровне значении остальных независимых переменных.

Это означает, что при увеличении среднегодовой ставки по кредитам на 17,456 тыс. руб. объем прибыли увеличится на 93,14 тыс. руб.; при увеличении среднегодовой ставки по кредитам и ставки по депозитам на 11,124 тыс. руб. объем прибыли увеличится на 1,3 тыс. руб.

Долю влияния фактора в суммарном влиянии всех факторов можно оценить по величине дельта-коэффициентов j:

где - коэффициент парной корреляции между фактором j и зависимой переменной.

Влияние факторов на изменение объема прибыли повлияло так, что за счет изменения среднегодовой ставки по кредитам на 92,5% объем прибыли увеличится на 1,011 тыс. руб., за счет снижения ставки депозитов на 64,5% объем прибыли снизится на 0,01 тыс. руб.

4. Оценка надежности уравнения регрессии

Проверку значимости уравнения регрессии произведем на основе вычисления F-критерия Фишера:

По таблице определим критическое значение при =0,05 F ; m ; n - m -1 = F 0,05 ; 2 ; 7 =4,74. Т.к. F расч = 20,36 > F крит =4,74, то уравнение регрессии с вероятностью 95% можно считать статистически значимым. Анализ остатков позволяет получить представление, насколько хорошо подобрана сама модель. Согласно общим предположениям регрессионного анализа остатки должны вести себя как независимые одинаково распределенные случайные величины. Проверку независимости остатков проведем с помощью критерия Дарбина-Уотсона (данные в табл. 2.4 столбцы 7,9)

DW близко к 2, значит, автокорреляция отсутствует. Для точного определения наличия автокорреляции используют критические значения d low и d high из таблицы, при =0,05, n =10, k =2:

d low =0,697 d high =1,641

Получаем, что d high < DW < 4-d high (1,641 < 2,350 < 2,359), можно сделать вывод об отсутствии автокорреляции. Это является одним из подтверждений высокого качества модели построенного по МНК.

5. Оценка с помощью t -критерия Стьюдента статистической значимости коэффициентов уравнения регрессии

Значимость коэффициентов уравнения регрессии а 0 , а 1 , а 2 оценим с использованием t -критерия Стьюдента.

b 11 =58,41913

b 22 =0,00072

b 33 =0,00178

Стандартная ошибка =6,19 (табл.2.5 строка 4)

Расчетные значения t -критерия Стьюдента приведены в табл.2.7 столбец 4.

Табличное значение t -критерия при 5% уровне значимости и степенях свободы

n - m - 1 = 10 - 2 - 1 = 7 =2,365

Если расчетное значение по модулю больше критического, то делается вывод о статистической значимости коэффициента регрессии, в противном случае коэффициенты регрессии статистически не значимы.

Так как <t кр, то коэффициенты регрессии а 0 , а 2 незначимы.

Так как >t кр, то коэффициент регрессии а 1 значим.

6. Построение точечного и интервального прогноза результирующего показателя

Прогнозные значения X 1,11 и X 2,11 можно определить с помощью методов экспертных оценок, с помощью средних абсолютных приростов или вычислить на основе экстраполяционных методов.

В качестве прогнозных оценок для Х 1 и Х 2 возьмем среднее значение каждой переменной увеличенное на 5% х 1 =42,41,05=44,52; х 2 =160,81,05=168,84.

Подставим в нее значения прогнозных факторов Х 1 и Х 2 .

у (х р ) = 33,295+0,76744,52+0,017168,84=70,365

Доверительный интервал прогноза будет иметь следующие границы.

Верхняя граница прогноза: у (х р ) + u

Нижняя граница прогноза: у (х р ) - u

u =S e t кр, S e = 6,19 (табл.2.5 строка 4)

t кр = 2,365 (при =0,05)

= (1; 44,52; 168,84)

u =6, 192,365=7,258

Результат прогноза представлен в таблице 2.8.

Таблица 2.8

	Нижняя граница	Верхняя граница
	70,365 - 7,258=63,107	70,365 + 7,258=77,623

7. Результаты расчетов отражены на графике:

Построена модель множественной регрессии зависимости объема прибыли У от ставки по депозитам Х 1 и внутрибанковским расходам Х 2:

у = 33,295 + 0,767х 1 + 0,017х 2

Коэффициент детерминации R 2 =0,855 свидетельствует о сильной зависимости факторов. В модели отсутствует автокорреляция остатков. Т.к. F расч =20,36 > F крит =7,74, то уравнение регрессии с вероятностью 95% можно считать статистически значимым.

Величина прибыли при неизменных условиях с вероятностью 95% будет находиться в интервале от 63,107 до 77,623.

Эти факторы тесно связаны между собой, что свидетельствует о наличии мультиколлинеарности. Параметры множественной регрессии теряют экономический смысл, оценки параметров ненадежны. Модель непригодна для анализа и прогнозирования. Включение факторов в модель статистически не оправдано. Причиной неадекватности модели послужили ошибки в организации, даны недостоверные или не учтены факторы в модели, погрешности в задании исходных данных.

Анализ показал, что зависимая переменная, то есть объем прибыли, имеет тесную связь с индексом ставки по кредитам и индексом размера внутрибанковских расходов. В результате чего кредитным учреждениям следует уделить особое внимание на эти показатели, искать пути уменьшения и оптимизации внутрибанковских расходов и вести эффективные ставки по кредитам.

Сокращение расходов банка возможно за счет экономии административно-хозяйственных расходов и уменьшения стоимости привлекаемых пассивов.

Экономия расходов может предусматривать сокращение персонала или уменьшение заработной платы, закрытие убыточных дополнительных офисов и филиалов.

Список литературы

1. Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов. - М.: ЮНИТИ - ДАНА, 2003.

2. Магнус Я.Р., Катышев П.К., Персецкий А.А. Эконометрика. Начальный курс. - М.: Дело, 2001.

3. Бородич С.А. эконометрика: Учеб. Пособие. - Мн.: Новое знание, 2006.

4. Елисеева И.И. Эконометрика: Учебник. - М., 2010.

Размещено на Allbest.ru

...

Подобные документы

Выбор факторных признаков для построения регрессионной модели неоднородных экономических процессов. Построение диаграммы рассеяния. Анализ матрицы коэффициентов парной корреляции. Определение коэффициентов детерминации и средних ошибок аппроксимации.

контрольная работа , добавлен 21.03.2015


Выбор факторных признаков для двухфакторной модели с помощью корреляционного анализа. Расчет коэффициентов регрессии, корреляции и эластичности. Построение модели линейной регрессии производительности труда от факторов фондо- и энерговооруженности.

задача , добавлен 20.03.2010


Проектирование регрессионной модели по панельным данным. Скрытые переменные и индивидуальные эффекты. Расчет коэффициентов однонаправленной модели с фиксированными эффектами по панельным данным в MS Excel. Выбор переменных для построения данной регрессии.

курсовая работа , добавлен 26.08.2013


Группировка предприятий по среднегодовой стоимости производственных фондов. Сглаживание скользящей средней и ее центрирование. Определение коэффициента линейной регрессионной модели и показателей детерминации. Коэффициенты эластичности и их интерпретация.

контрольная работа , добавлен 06.05.2015


Расчет параметров линейного уравнения множественной регрессии; определение сравнительной оценки влияния факторов на результативный показатель с помощью коэффициентов эластичности и прогнозного значения результата; построение регрессионной модели.

контрольная работа , добавлен 29.03.2011


Построение и анализ классической многофакторной линейной эконометрической модели. Вид линейной двухфакторной модели, её оценка в матричной форме и проверка адекватности по критерию Фишера. Расчет коэффициентов множественной детерминации и корреляции.

контрольная работа , добавлен 01.06.2010


Построение линейной модели зависимости цены товара в торговых точках. Расчет матрицы парных коэффициентов корреляции, оценка статистической значимости коэффициентов корреляции, параметров регрессионной модели, доверительного интервала для наблюдений.

лабораторная работа , добавлен 17.10.2009


Определение методом регрессионного и корреляционного анализа линейных и нелинейных связей между показателями макроэкономического развития. Расчет среднего арифметического по столбцам таблицы. Определение коэффициента корреляции и уравнения регрессии.

контрольная работа , добавлен 14.06.2014


Проведение анализа экономической деятельности предприятий отрасли: расчет параметров линейного уравнения множественной регрессии с полным перечнем факторов, оценка статистической значимости параметров регрессионной модели, расчет прогнозных значений.

лабораторная работа , добавлен 01.07.2010


Порядок построения линейного регрессионного уравнения, вычисление его основных параметров и дисперсии переменных, средней ошибки аппроксимации и стандартной ошибки остаточной компоненты. Построение линии показательной зависимости на поле корреляции.

В предыдущих заметках предметом анализа часто становилась отдельная числовая переменная, например, доходность взаимных фондов, время загрузки Web-страницы или объем потребления безалкогольных напитков. В настоящей и следующих заметках мы рассмотрим методы предсказания значений числовой переменной в зависимости от значений одной или нескольких других числовых переменных.

Материал будет проиллюстрирован сквозным примером. Прогнозирование объема продаж в магазине одежды. Сеть магазинов уцененной одежды Sunflowers на протяжении 25 лет постоянно расширялась. Однако в настоящее время у компании нет систематического подхода к выбору новых торговых точек. Место, в котором компания собирается открыть новый магазин, определяется на основе субъективных соображений. Критериями выбора являются выгодные условия аренды или представления менеджера об идеальном местоположении магазина. Представьте, что вы - руководитель отдела специальных проектов и планирования. Вам поручили разработать стратегический план открытия новых магазинов. Этот план должен содержать прогноз годового объема продаж во вновь открываемых магазинах. Вы полагаете, что торговая площадь непосредственно связана с объемом выручки, и хотите учесть этот факт в процессе принятия решения. Как разработать статистическую модель, позволяющую прогнозировать годовой объем продаж на основе размера нового магазина?

Как правило, для предсказания значений переменной используется регрессионный анализ. Его цель - разработать статистическую модель, позволяющую предсказывать значения зависимой переменной, или отклика, по значениям, по крайней мере одной, независимой, или объясняющей, переменной. В настоящей заметке мы рассмотрим простую линейную регрессию - статистический метод, позволяющий предсказывать значения зависимой переменной Y по значениям независимой переменной X . В последующих заметках будет описана модель множественной регрессии, предназначенная для предсказания значений независимой переменной Y по значениям нескольких зависимых переменных (Х 1 , Х 2 , …, X k ).

Скачать заметку в формате или , примеры в формате

Виды регрессионных моделей

где ρ 1 – коэффициент автокорреляции; если ρ 1 = 0 (нет автокорреляции), D ≈ 2; если ρ 1 ≈ 1 (положительная автокорреляции), D ≈ 0; если ρ 1 = -1 (отрицательная автокорреляции), D ≈ 4.

На практике применение критерия Дурбина-Уотсона основано на сравнении величины D с критическими теоретическими значениями d L и d U для заданного числа наблюдений n , числа независимых переменных модели k (для простой линейной регрессии k = 1) и уровня значимости α. Если D < d L , гипотеза о независимости случайных отклонений отвергается (следовательно, присутствует положительная автокорреляция); если D > d U , гипотеза не отвергается (то есть автокорреляция отсутствует); если d L < D < d U , нет достаточных оснований для принятия решения. Когда расчётное значение D превышает 2, то с d L и d U сравнивается не сам коэффициент D , а выражение (4 – D ).

Для вычисления статистики Дурбина-Уотсона в Excel обратимся к нижней таблице на рис. 14 Вывод остатка . Числитель в выражении (10) вычисляется с помощью функции =СУММКВРАЗН(массив1;массив2), а знаменатель =СУММКВ(массив) (рис. 16).

Рис. 16. Формулы расчета статистики Дурбина-Уотсона

В нашем примере D = 0,883. Основной вопрос заключается в следующем - какое значение статистики Дурбина-Уотсона следует считать достаточно малым, чтобы сделать вывод о существовании положительной автокорреляции? Необходимо соотнести значение D с критическими значениями (d L и d U ), зависящими от числа наблюдений n и уровня значимости α (рис. 17).

Рис. 17. Критические значения статистики Дурбина-Уотсона (фрагмент таблицы)

Таким образом, в задаче об объеме продаж в магазине, доставляющем товары на дом, существуют одна независимая переменная (k = 1), 15 наблюдений (n = 15) и уровень значимости α = 0,05. Следовательно, d L = 1,08 и d U = 1,36. Поскольку D = 0,883 < d L = 1,08, между остатками существует положительная автокорреляция, метод наименьших квадратов применять нельзя.

Проверка гипотез о наклоне и коэффициенте корреляции

Выше регрессия применялась исключительно для прогнозирования. Для определения коэффициентов регрессии и предсказания значения переменной Y при заданной величине переменной X использовался метод наименьших квадратов. Кроме того, мы рассмотрели среднеквадратичную ошибку оценки и коэффициент смешанной корреляции. Если анализ остатков подтверждает, что условия применимости метода наименьших квадратов не нарушаются, и модель простой линейной регрессии является адекватной, на основе выборочных данных можно утверждать, что между переменными в генеральной совокупности существует линейная зависимость.

Применение t -критерия для наклона. Проверяя, равен ли наклон генеральной совокупности β 1 нулю, можно определить, существует ли статистически значимая зависимость между переменными X и Y . Если эта гипотеза отклоняется, можно утверждать, что между переменными X и Y существует линейная зависимость. Нулевая и альтернативная гипотезы формулируются следующим образом: Н 0: β 1 = 0 (нет линейной зависимости), Н1: β 1 ≠ 0 (есть линейная зависимость). По определению t -статистика равна разности между выборочным наклоном и гипотетическим значением наклона генеральной совокупности, деленной на среднеквадратичную ошибку оценки наклона:

(11) t = (b 1 – β 1 ) / S b 1

где b 1 – наклон прямой регрессии по выборочным данным, β1 – гипотетический наклон прямой генеральной совокупности, , а тестовая статистика t имеет t -распределение с n – 2 степенями свободы.

Проверим, существует ли статистически значимая зависимость между размером магазина и годовым объемом продаж при α = 0,05. t -критерий выводится наряду с другими параметрами при использовании Пакета анализа (опция Регрессия ). Полностью результаты работы Пакета анализа приведены на рис. 4, фрагмент, относящийся к t-статистике – на рис. 18.

Рис. 18. Результаты применения t

Поскольку число магазинов n = 14 (см. рис.3), критическое значение t -статистики при уровне значимости α = 0,05 можно найти по формуле: t L =СТЬЮДЕНТ.ОБР(0,025;12) = –2,1788, где 0,025 – половина уровня значимости, а 12 = n – 2; t U =СТЬЮДЕНТ.ОБР(0,975;12) = +2,1788.

Поскольку t -статистика = 10,64 > t U = 2,1788 (рис. 19), нулевая гипотеза Н 0 отклоняется. С другой стороны, р -значение для Х = 10,6411, вычисляемое по формуле =1-СТЬЮДЕНТ.РАСП(D3;12;ИСТИНА), приближенно равно нулю, поэтому гипотеза Н 0 снова отклоняется. Тот факт, что р -значение почти равно нулю, означает, что если бы между размерами магазинов и годовым объемом продаж не существовало реальной линейной зависимости, обнаружить ее с помощью линейной регрессии было бы практически невозможно. Следовательно, между средним годовым объемом продаж в магазинах и их размером существует статистически значимая линейная зависимость.

Рис. 19. Проверка гипотезы о наклоне генеральной совокупности при уровне значимости, равном 0,05, и 12 степенях свободы

Применение F -критерия для наклона. Альтернативным подходом к проверке гипотез о наклоне простой линейной регрессии является использование F -критерия. Напомним, что F -критерий применяется для проверки отношения между двумя дисперсиями (подробнее см. ). При проверке гипотезы о наклоне мерой случайных ошибок является дисперсия ошибки (сумма квадратов ошибок, деленная на количество степеней свободы), поэтому F -критерий использует отношение дисперсии, объясняемой регрессией (т.е. величины SSR , деленной на количество независимых переменных k ), к дисперсии ошибок (MSE = S Y X 2 ).

По определению F -статистика равна среднему квадрату отклонений, обусловленных регрессией (MSR), деленному на дисперсию ошибки (MSE): F = MSR / MSE , где MSR = SSR / k , MSE = SSE /(n – k – 1), k – количество независимых переменных в регрессионной модели. Тестовая статистика F имеет F -распределение с k и n – k – 1 степенями свободы.

При заданном уровне значимости α решающее правило формулируется так: если F > F U , нулевая гипотеза отклоняется; в противном случае она не отклоняется. Результаты, оформленные в виде сводной таблицы дисперсионного анализа, приведены на рис. 20.

Рис. 20. Таблица дисперсионного анализа для проверки гипотезы о статистической значимости коэффициента регрессии

Аналогично t -критерию F -критерий выводится в таблицу при использовании Пакета анализа (опция Регрессия ). Полностью результаты работы Пакета анализа приведены на рис. 4, фрагмент, относящийся к F -статистике – на рис. 21.

Рис. 21. Результаты применения F -критерия, полученные с помощью Пакета анализа Excel

F-статистика равна 113,23, а р -значение близко к нулю (ячейка Значимость F ). Если уровень значимости α равен 0,05, определить критическое значение F -распределения с одной и 12 степенями свободы можно по формуле F U =F.ОБР(1-0,05;1;12) = 4,7472 (рис. 22). Поскольку F = 113,23 > F U = 4,7472, причем р -значение близко к 0 < 0,05, нулевая гипотеза Н 0 отклоняется, т.е. размер магазина тесно связан с его годовым объемом продаж.

Рис. 22. Проверка гипотезы о наклоне генеральной совокупности при уровне значимости, равном 0,05, с одной и 12 степенями свободы

Доверительный интервал, содержащий наклон β 1 . Для проверки гипотезы о существовании линейной зависимости между переменными можно построить доверительный интервал, содержащий наклон β 1 и убедиться, что гипотетическое значение β 1 = 0 принадлежит этому интервалу. Центром доверительного интервала, содержащего наклон β 1 , является выборочный наклон b 1 , а его границами - величины b 1 ± t n –2 S b 1

Как показано на рис. 18, b 1 = +1,670, n = 14, S b 1 = 0,157. t 12 =СТЬЮДЕНТ.ОБР(0,975;12) = 2,1788. Следовательно, b 1 ± t n –2 S b 1 = +1,670 ± 2,1788 * 0,157 = +1,670 ± 0,342, или + 1,328 ≤ β 1 ≤ +2,012. Таким образом, наклон генеральной совокупности с вероятностью 0,95 лежит в интервале от +1,328 до +2,012 (т.е. от 1 328 000 до 2 012 000 долл.). Поскольку эти величины больше нуля, между годовым объемом продаж и площадью магазина существует статистически значимая линейная зависимость. Если бы доверительный интервал содержал нуль, между переменными не было бы зависимости. Кроме того, доверительный интервал означает, что каждое увеличение площади магазина на 1 000 кв. футов приводит к увеличению среднего объема продаж на величину от 1 328 000 до 2 012 000 долларов.

Использование t -критерия для коэффициента корреляции. был введен коэффициент корреляции r , представляющий собой меру зависимости между двумя числовыми переменными. С его помощью можно установить, существует ли между двумя переменными статистически значимая связь. Обозначим коэффициент корреляции между генеральными совокупностями обеих переменных символом ρ. Нулевая и альтернативная гипотезы формулируются следующим образом: Н 0 : ρ = 0 (нет корреляции), Н 1 : ρ ≠ 0 (есть корреляция). Проверка существования корреляции:

где r = + , если b 1 > 0, r = – , если b 1 < 0. Тестовая статистика t имеет t -распределение с n – 2 степенями свободы.

В задаче о сети магазинов Sunflowers r 2 = 0,904, а b 1 - +1,670 (см. рис. 4). Поскольку b 1 > 0, коэффициент корреляции между объемом годовых продаж и размером магазина равен r = +√0,904 = +0,951. Проверим нулевую гипотезу, утверждающую, что между этими переменными нет корреляции, используя t -статистику:

При уровне значимости α = 0,05 нулевую гипотезу следует отклонить, поскольку t = 10,64 > 2,1788. Таким образом, можно утверждать, что между объемом годовых продаж и размером магазина существует статистически значимая связь.

При обсуждении выводов, касающихся наклона генеральной совокупности, доверительные интервалы и критерии для проверки гипотез являются взаимозаменяемыми инструментами. Однако вычисление доверительного интервала, содержащего коэффициент корреляции, оказывается более сложным делом, поскольку вид выборочного распределения статистики r зависит от истинного коэффициента корреляции.

Оценка математического ожидания и предсказание индивидуальных значений

В этом разделе рассматриваются методы оценки математического ожидания отклика Y и предсказания индивидуальных значений Y при заданных значениях переменной X .

Построение доверительного интервала. В примере 2 (см. выше раздел Метод наименьших квадратов ) регрессионное уравнение позволило предсказать значение переменной Y X . В задаче о выборе места для торговой точки средний годовой объем продаж в магазине площадью 4000 кв. футов был равен 7,644 млн. долл. Однако эта оценка математического ожидания генеральной совокупности является точечной. для оценки математического ожидания генеральной совокупности была предложена концепция доверительного интервала. Аналогично можно ввести понятие доверительного интервала для математического ожидания отклика при заданном значении переменной X :

где , = b 0 + b 1 X i – предсказанное значение переменное Y при X = X i , S YX – среднеквадратичная ошибка, n – объем выборки, X i - заданное значение переменной X , µ Y | X = X i – математическое ожидание переменной Y при Х = Х i , SSX =

Анализ формулы (13) показывает, что ширина доверительного интервала зависит от нескольких факторов. При заданном уровне значимости возрастание амплитуды колебаний вокруг линии регрессии, измеренное с помощью среднеквадратичной ошибки, приводит к увеличению ширины интервала. С другой стороны, как и следовало ожидать, увеличение объема выборки сопровождается сужением интервала. Кроме того, ширина интервала изменяется в зависимости от значений X i . Если значение переменной Y предсказывается для величин X , близких к среднему значению , доверительный интервал оказывается уже, чем при прогнозировании отклика для значений, далеких от среднего.

Допустим, что, выбирая место для магазина, мы хотим построить 95%-ный доверительный интервал для среднего годового объема продаж во всех магазинах, площадь которых равна 4000 кв. футов:

Следовательно, средний годовой объем продаж во всех магазинах, площадь которых равна 4 000 кв. футов, с 95% -ной вероятностью лежит в интервале от 6,971 до 8,317 млн. долл.

Вычисление доверительного интервала для предсказанного значения. Кроме доверительного интервала для математического ожидания отклика при заданном значении переменной X , часто необходимо знать доверительный интервал для предсказанного значения. Несмотря на то что формула для вычисления такого доверительного интервала очень похожа на формулу (13), этот интервал содержит предсказанное значение, а не оценку параметра. Интервал для предсказанного отклика Y X = Xi при конкретном значении переменной X i определяется по формуле:

Предположим, что, выбирая место для торговой точки, мы хотим построить 95%-ный доверительный интервал для предсказанного годового объема продаж в магазине, площадь которого равна 4000 кв. футов:

Следовательно, предсказанный годовой объем продаж в магазине, площадь которого равна 4000 кв. футов, с 95%-ной вероятностью лежит в интервале от 5,433 до 9,854 млн. долл. Как видим, доверительный интервал для предсказанного значения отклика намного шире, чем доверительный интервал для его математического ожидания. Это объясняется тем, что изменчивость при прогнозировании индивидуальных значений намного больше, чем при оценке математического ожидания.

Подводные камни и этические проблемы, связанные с применением регрессии

Трудности, связанные с регрессионным анализом:

• Игнорирование условий применимости метода наименьших квадратов.
• Ошибочная оценка условий применимости метода наименьших квадратов.
• Неправильный выбор альтернативных методов при нарушении условий применимости метода наименьших квадратов.
• Применение регрессионного анализа без глубоких знаний о предмете исследования.
• Экстраполяция регрессии за пределы диапазона изменения объясняющей переменной.
• Путаница между статистической и причинно-следственной зависимостями.

Широкое распространение электронных таблиц и программного обеспечения для статистических расчетов ликвидировало вычислительные проблемы, препятствовавшие применению регрессионного анализа. Однако это привело к тому, что регрессионный анализ стали применять пользователи, не обладающие достаточной квалификацией и знаниями. Откуда пользователям знать об альтернативных методах, если многие из них вообще не имеют ни малейшего понятия об условиях применимости метода наименьших квадратов и не умеют проверять их выполнение?

Исследователь не должен увлекаться перемалыванием чисел - вычислением сдвига, наклона и коэффициента смешанной корреляции. Ему нужны более глубокие знания. Проиллюстрируем это классическим примером, взятым из учебников. Анскомб показал, что все четыре набора данных, приведенных на рис. 23, имеют одни и те же параметры регрессии (рис. 24).

Рис. 23. Четыре набора искусственных данных

Рис. 24. Регрессионный анализ четырех искусственных наборов данных; выполнен с помощью Пакета анализа (кликните на рисунке, чтобы увеличить изображение)

Итак, с точки зрения регрессионного анализа все эти наборы данных совершенно идентичны. Если бы анализ был на этом закончен, мы потеряли бы много полезной информации. Об этом свидетельствуют диаграммы разброса (рис. 25) и графики остатков (рис. 26), построенные для этих наборов данных.

Рис. 25. Диаграммы разброса для четырех наборов данных

Диаграммы разброса и графики остатков свидетельствуют о том, что эти данные отличаются друг от друга. Единственный набор, распределенный вдоль прямой линии, - набор А. График остатков, вычисленных по набору А, не имеет никакой закономерности. Этого нельзя сказать о наборах Б, В и Г. График разброса, построенный по набору Б, демонстрирует ярко выраженную квадратичную модель. Этот вывод подтверждается графиком остатков, имеющим параболическую форму. Диаграмма разброса и график остатков показывают, что набор данных В содержит выброс. В этой ситуации необходимо исключить выброс из набора данных и повторить анализ. Метод, позволяющий обнаруживать и исключать выбросы из наблюдений, называется анализом влияния. После исключения выброса результат повторной оценки модели может оказаться совершенно иным. Диаграмма разброса, построенная по данным из набора Г, иллюстрирует необычную ситуацию, в которой эмпирическая модель значительно зависит от отдельного отклика (Х 8 = 19, Y 8 = 12,5). Такие регрессионные модели необходимо вычислять особенно тщательно. Итак, графики разброса и остатков являются крайне необходимым инструментом регрессионного анализа и должны быть его неотъемлемой частью. Без них регрессионный анализ не заслуживает доверия.

Рис. 26. Графики остатков для четырех наборов данных

Как избежать подводных камней при регрессионном анализе:

• Анализ возможной взаимосвязи между переменными X и Y всегда начинайте с построения диаграммы разброса.
• Прежде чем интерпретировать результаты регрессионного анализа, проверяйте условия его применимости.
• Постройте график зависимости остатков от независимой переменной. Это позволит определить, насколько эмпирическая модель соответствует результатам наблюдения, и обнаружить нарушение постоянства дисперсии.
• Для проверки предположения о нормальном распределении ошибок используйте гистограммы, диаграммы «ствол и листья», блочные диаграммы и графики нормального распределения.
• Если условия применимости метода наименьших квадратов не выполняются, используйте альтернативные методы (например, модели квадратичной или множественной регрессии).
• Если условия применимости метода наименьших квадратов выполняются, необходимо проверить гипотезу о статистической значимости коэффициентов регрессии и построить доверительные интервалы, содержащие математическое ожидание и предсказанное значение отклика.
• Избегайте предсказывать значения зависимой переменной за пределами диапазона изменения независимой переменной.
• Имейте в виду, что статистические зависимости не всегда являются причинно-следственными. Помните, что корреляция между переменными не означает наличия причинно-следственной зависимости между ними.

Резюме. Как показано на структурной схеме (рис. 27), в заметке описаны модель простой линейной регрессии, условия ее применимости и способы проверки этих условий. Рассмотрен t -критерий для проверки статистической значимости наклона регрессии. Для предсказания значений зависимой переменной использована регрессионная модель. Рассмотрен пример, связанный с выбором места для торговой точки, в котором исследуется зависимость годового объема продаж от площади магазина. Полученная информация позволяет точнее выбрать место для магазина и предсказать его годовой объем продаж. В следующих заметках будет продолжено обсуждение регрессионного анализа, а также рассмотрены модели множественной регрессии.

Рис. 27. Структурная схема заметки

Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 792–872

Если зависимая переменная является категорийной, необходимо применять логистическую регрессию.

16.1 Простая линейная регрессия

Чтобы вызвать регрессионный анализ в SPSS, выберите в меню Analyze... (Анализ) Regression... (Регрессия). Откроется соответствующее подменю.

Рис. 16.1:

При изучении линейного регрессионного анализа снова будут проведено различие между простым анализом (одна независимая переменная) и множественным анализом (несколько независимых переменных). Никаких принципиальных отличий между этими видами регрессии нет, однако простая линейная регрессия является простейшей и применяется чаще всех остальных видов.

Этот вид регрессии лучше всего подходит для того, чтобы продемонстрировать основополагающие принципы регрессионного анализа. Рассмотрим пример из раздела корреляционный анализ с зависимостью показателя холестерина спустя один месяц после начала лечения от исходного показателя. Можно легко заметить очевидную связь: обе переменные развиваются в одном направлении и множество точек, соответствующих наблюдаемым значениям показателей, явно концентрируется (за некоторыми исключениями) вблизи прямой (прямой регрессии). В таком случае говорят о линейной связи.

у = b х + а ,
где b - регрессионные коэффициенты, a - смещение по оси ординат (OY).

Смещение по оси ординат соответствует точке на оси Y (вертикальной оси), где прямая регрессии пересекает эту ось. Коэффициент регрессии b через соотношение:
b = tg(a) - указывает на угол наклона прямой.

При проведении простой линейной регрессии основной задачей является определение параметров b и а. Оптимальным решением этой задачи является такая прямая, для которой сумма квадратов вертикальных расстояний до отдельных точек данных является минимальной.

Если мы рассмотрим показатель холестерина через один месяц (переменная chol1 ) как зависимую переменную (у), а исходную величину как независимую переменную (х), то тогда для проведения регрессионного анализа нужно будет определить параметры соотношения:
chol1 = b chol0 + a

После определения этих параметров, зная исходный показатель холестерина, можно спрогнозировать показатель, который будет через один месяц.

Расчёт уравнения регрессии

Выберите в меню Analyze... (Анализ) Regression...(Регрессия) Linear... (Линейная). Появится диалоговое окно Linear Regression (Линейная регрессия).

Перенесите переменную chol1 в поле для зависимых переменных и присвойте переменной chol0 статус независимой переменной.

Ничего больше не меняя, начните расчёт нажатием ОК.

Рис.16.2

Вывод основных результатов выглядит следующим образом:

Model Summary (Сводная таблица по модели)

Model (Модель)	R	R Square (R-квадрат)	Adjusted R Square (Скорректир. R-квадрат)	Std. Error of the Estimate (Стандартная ошибка оценки)
1	,861 а	,741	,740	25,26

а. Predictors: (Constant), Cholesterin, Ausgangswert (Влияющие переменные: (константы), холестерин, исходная величина)

Model (Модель)		Sum of Squares (Сумма Квадратов)	df	Mean Square (Среднее значение квадрата)	F	Sig. (Значимость)
1	Regression (Регрессия)	314337,948	1	314337,9	492,722	,000 a
	Residual (Остатки)	109729,408	172	637,962
	Total (Сумма)	424067,356	173

a. Predictors: (Constant), Cholesterin, Ausgangswert (Влияющие переменные: (константа), холестерин, исходная величина).
b. Dependent Variable: Cholesterin, nach 1 Monat (Зависимая переменная холестерин через 1 месяц)

Coefficients (Коэффициенты) а

Model (Модель)		Unstandardized Coefficients			t	Sig. (Значимость)
		B	Std: Error (Станд. ошибка)	ß (Beta)
1	(Constant) (Константа)	34,546	9,416		3,669	,000
	Cholesterin, Ausgangswert	,863	,039	,861	22,197	,000

a. Dependent Variable (Зависимая переменная)

Рассмотрим сначала нижнюю часть результатов расчётов. Здесь выводятся коэффициент регрессии b и смещение по оси ординат а под именем "константа". То есть, уравнение регрессии выглядит следующим образом:

chol1 = 0,863 chol0 + 34,546

Если значение исходного показателя холестерина составляет, к примеру, 280, то через один месяц можно ожидать показатель равный 276.

Частные рассчитанных коэффициентов и их стандартная ошибка дают контрольную величину Т; соответственный уровень значимости относится к существованию ненулевых коэффициентов регрессии. Значение коэффициента ß будет рассмотрено при изучении многомерного анализа .

Средняя часть расчётов отражает два источника дисперсии: дисперсию, которая описывается уравнением регрессии (сумма квадратов, обусловленная регрессией) и дисперсию, которая не учитывается при записи уравнения (остаточная сумма квадратов). Частное от суммы квадратов, обусловленных регрессией и остаточной суммы квадратов называется "коэфициентом детерминации". В таблице результатов это частное выводится под именем "R-квадрат". В нашем примере мера определённости равна:

314337,948 / 424067,356 = 0,741

Эта величина характеризует качество регрессионной прямой, то есть степень соответствия между регрессионной моделью и исходными данными. Мера определённости всегда лежит в диапазоне от 0 до 1. Существование ненулевых коэффициентов регрессии проверяется посредством вычисления контрольной величины F, к которой относится соответствующий уровень значимости.

В простом линейном регрессионном анализе квадратный корень из коэфициента детерминации, обозначаемый "R", равен корреляционному коэффициенту Пирсона. При множественном анализе эта величина менее наглядна, нежели сам коэфициент детерминации. Величина "Cмещенный R-квадрат" всегда меньше, чем несмещенный. При наличии большого количества независимых переменных, мера определённости корректируется в сторону уменьшения. Принципиальный вопрос о том, может ли вообще имеющаяся связь между переменными рассматриваться как линейная, проще и нагляднее всего решать, глядя на соответствующую диаграмму рассеяния. Кроме того, в пользу гипотезы о линейной связи говорит также высокий уровень дисперсии, описываемой уравнением регрессии.

И, наконец, стандартизированные прогнозируемые значения и стандартизированные остатки можно предоставить в виде графика. Вы получите этот график, если через кнопку Plots...(Графики) зайдёте в соответствующее диалоговое окно и зададите в нём параметры *ZRESID и *ZPRED в качестве переменных, отображаемых по осям у и х соответственно. В случае линейной регрессии остатки распределяются случайно по обе стороны от горизонтальной нулевой линии.

Сохранение новых переменных

Многочисленные вспомогательные значения, рассчитываемые в ходе построения уравнения регрессии, можно сохранить как переменные и использовать в дальнейших расчётах.

Для этого в диалоговом окне Linear Regression (Линейная регрессия) щёлкните на кнопке Save (Сохранить). Откроется диалоговое окно Linear Regression: Save (Линейная регрессия: Сохранение) как изображено на рисунке 16.3.

Рис. 16.3:

Интересными здесь представляются опции Standardized (Стандартизированные значения) и Unstandardized (Нестандартизированные значения), которые находятся под рубрикой Predicted values (Прогнозируемые величины опции). При выборе опции Не стандартизированные значения будут рассчитывается значения у, которое соответствуют уравнению регрессии. При выборе опции Стандартизированные значения прогнозируемая величина нормализуется. SPSS автоматически присваивает новое имя каждой новообразованной переменной, независимо от того, рассчитываете ли Вы прогнозируемые значения, расстояния, прогнозируемые интервалы, остатки или какие-либо другие важные статистические характеристики. Нестандартизированным значениям SPSS присваивает имена pre_1 (predicted value), pre_2 и т.д., а стандартизированным zpr_l.

Щёлкните в диалоговом окне Linear Regression: Save (Линейная регрессия: Сохранение) в поле Predicted values (Прогнозируемые значения) на опции Unstandardized (Нестандартизированные значения).

В редакторе данных будет образована новая переменная под именем рrе_1 и добавлена в конец списка переменных в файле. Для объяснения значений, находящихся в переменной рrе_1 , возьмём случай 5. Для случая 5 переменная рrе_1 содержит нестандартизированное прогнозируемое значение 263,11289. Это прогнозируемое значение слегка отличается в сторону увеличения от реального показателя содержания холестерина, взятого через один месяц (chol1 ) и равного 260. Нестандартизированное прогнозируемое значение для переменной chol1 , так же как и другие значения переменной рге_1, было вычислено исходя из соответствующего уравнения регрессии.

Если мы в уравнение регрессии:

chol1 = 0,863 chol0 + 34,546

подставим исходное значение для chol0 (265), то получим: chol1 = 0,863 265 + 34,546 = 263,241

Небольшое отклонение от значения, хранящегося в переменной рге_1 объясняется тем, что SPSS использует в расчётах более точные значения, чем те, которые выводятся в окне просмотра результатов.

Добавьте для этого в конец файла hyper.sav , ещё два случая, используя фиктивные значения для переменной chol0. Пусть к примеру, это будут значения 282 и 314.

Мы исходим из того, что нам не известны значения показателя холестерина через месяц после начала лечения, и мы хотим спрогнозировать значение переменной chol1 .

Оставьте предыдущие установки без изменений и проведите новый расчёт уравнения регрессии.

В конце списка переменных добавится переменная рге_2. Для нового добавленного случая (№175) для переменной chol1 будет предсказано значение 277,77567, а для случая №176 - значение 305,37620.

Построение регрессионной прямой

Чтобы на диаграмме рассеяния изобразить регрессионную прямую, поступите следующим образом:

Рис. 16.9:

Выбор осей

Для диаграмм рассеяния часто оказывается необходимой дополнительная корректировка осей. Продемонстрируем такую коррекцию при помощи одного примера. В файле raucher.sav находятся десять фиктивных наборов данных. Переменная konsum указывает на количество сигарет, которые выкуривает один человек в день, а переменная puls на количество времени, необходимое каждому испытуемому для восстановления пульса до нормальной частоты после двадцати приседаний. Как было показано ранее, постройте диаграмму рассеяния с внедрённой регрессионной прямой.

В диалоговом окне Simple Scatterplot (Простая диаграмма рассеяния) перенесите переменную puls в поле оси Y, а переменную konsum - в поле оси X. После соответствующей обработки данных в окне просмотра появится диаграмма рассеяния, изображённая на рисунке 16.10.

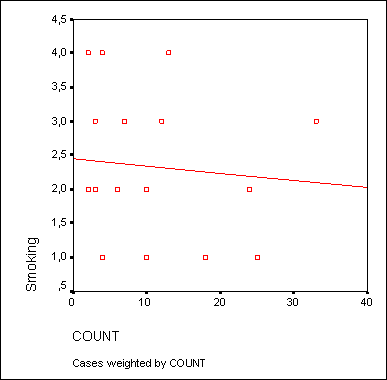
Рис. 16.10:

Так как никто не выкуривает минус 10 сигарет в день, точка начала отсчёта оси X является не совсем корректной. Поэтому эту ось необходимо откорректировать.

В окне просмотра Вы увидите откорректированную диаграмму рассеяния (см. рис. 16.13).

Рис. 16.13:

На откорректированной диаграмме рассеяния теперь стало проще распознать начальную точку на оси Y, которая образуется при пересечении с регрессионной прямой. Значение этой точки примерно равно 2,9. Сравним это значение с уравнением регрессии для переменных puls (зависимая переменная) и konsum (независимая переменная). В результате расчёта уравнения регрессии в окне отображения результатов появятся следующие значения:

Coefficients (Коэффициенты) а

Model (Модель)		Unstandardized Coefficients (Не стандартизированные коэффициенты)		Standardized Coefficients (Стандартизированные коэффициенты)	t	Sig. (Значимость)
		B	Std: Error (Станд. ошибка)	ß (Beta)
1	(Constant) (Константа)	2,871	,639		4,492	,002
	tgl. Zigarettenkonsum	,145	,038	,804	3,829	,005

a. Dependent Variable: Pulsfrequenz unter 80 (Зависимая переменная: частота пульса ниже 80)

Что дает следующее уравнение регрессии:

puls = 0,145 konsum + 2,871

Константа в вышеприведенном уравнении регрессии (2,871) соответствует точке на оси Y, которая образуется в точке пересечения с регрессионной прямой.

Регрессионный анализ — это статистический метод исследования, позволяющий показать зависимость того или иного параметра от одной либо нескольких независимых переменных. В докомпьютерную эру его применение было достаточно затруднительно, особенно если речь шла о больших объемах данных. Сегодня, узнав как построить регрессию в Excel, можно решать сложные статистические задачи буквально за пару минут. Ниже представлены конкретные примеры из области экономики.

Виды регрессии

Само это понятие было введено в математику в 1886 году. Регрессия бывает:

• линейной;
• параболической;
• степенной;
• экспоненциальной;
• гиперболической;
• показательной;
• логарифмической.

Пример 1

Рассмотрим задачу определения зависимости количества уволившихся членов коллектива от средней зарплаты на 6 промышленных предприятиях.

Задача. На шести предприятиях проанализировали среднемесячную заработную плату и количество сотрудников, которые уволились по собственному желанию. В табличной форме имеем:

		Количество уволившихся	Зарплата
			30000 рублей
			35000 рублей
			40000 рублей
			45000 рублей
			50000 рублей
			55000 рублей
			60000 рублей

Для задачи определения зависимости количества уволившихся работников от средней зарплаты на 6 предприятиях модель регрессии имеет вид уравнения Y = а 0 + а 1 x 1 +…+а k x k , где х i — влияющие переменные, a i — коэффициенты регрессии, a k — число факторов.

Для данной задачи Y — это показатель уволившихся сотрудников, а влияющий фактор — зарплата, которую обозначаем X.

Использование возможностей табличного процессора «Эксель»

Анализу регрессии в Excel должно предшествовать применение к имеющимся табличным данным встроенных функций. Однако для этих целей лучше воспользоваться очень полезной надстройкой «Пакет анализа». Для его активации нужно:

• с вкладки «Файл» перейти в раздел «Параметры»;
• в открывшемся окне выбрать строку «Надстройки»;
• щелкнуть по кнопке «Перейти», расположенной внизу, справа от строки «Управление»;
• поставить галочку рядом с названием «Пакет анализа» и подтвердить свои действия, нажав «Ок».

Если все сделано правильно, в правой части вкладки «Данные», расположенном над рабочим листом «Эксель», появится нужная кнопка.

в Excel

Теперь, когда под рукой есть все необходимые виртуальные инструменты для осуществления эконометрических расчетов, можем приступить к решению нашей задачи. Для этого:

• щелкаем по кнопке «Анализ данных»;
• в открывшемся окне нажимаем на кнопку «Регрессия»;
• в появившуюся вкладку вводим диапазон значений для Y (количество уволившихся работников) и для X (их зарплаты);
• подтверждаем свои действия нажатием кнопки «Ok».

В результате программа автоматически заполнит новый лист табличного процессора данными анализа регрессии. Обратите внимание! В Excel есть возможность самостоятельно задать место, которое вы предпочитаете для этой цели. Например, это может быть тот же лист, где находятся значения Y и X, или даже новая книга, специально предназначенная для хранения подобных данных.

Анализ результатов регрессии для R-квадрата

В Excel данные полученные в ходе обработки данных рассматриваемого примера имеют вид:

Прежде всего, следует обратить внимание на значение R-квадрата. Он представляет собой коэффициент детерминации. В данном примере R-квадрат = 0,755 (75,5%), т. е. расчетные параметры модели объясняют зависимость между рассматриваемыми параметрами на 75,5 %. Чем выше значение коэффициента детерминации, тем выбранная модель считается более применимой для конкретной задачи. Считается, что она корректно описывает реальную ситуацию при значении R-квадрата выше 0,8. Если R-квадрата<0,5, то такой анализа регрессии в Excel нельзя считать резонным.

Анализ коэффициентов

Число 64,1428 показывает, каким будет значение Y, если все переменные xi в рассматриваемой нами модели обнулятся. Иными словами можно утверждать, что на значение анализируемого параметра оказывают влияние и другие факторы, не описанные в конкретной модели.

Следующий коэффициент -0,16285, расположенный в ячейке B18, показывает весомость влияния переменной Х на Y. Это значит, что среднемесячная зарплата сотрудников в пределах рассматриваемой модели влияет на число уволившихся с весом -0,16285, т. е. степень ее влияния совсем небольшая. Знак «-» указывает на то, что коэффициент имеет отрицательное значение. Это очевидно, так как всем известно, что чем больше зарплата на предприятии, тем меньше людей выражают желание расторгнуть трудовой договор или увольняется.

Множественная регрессия

Под таким термином понимается уравнение связи с несколькими независимыми переменными вида:

y=f(x 1 +x 2 +…x m) + ε, где y — это результативный признак (зависимая переменная), а x 1 , x 2 , …x m — это признаки-факторы (независимые переменные).

Оценка параметров

Для множественной регрессии (МР) ее осуществляют, используя метод наименьших квадратов (МНК). Для линейных уравнений вида Y = a + b 1 x 1 +…+b m x m + ε строим систему нормальных уравнений (см. ниже)

Чтобы понять принцип метода, рассмотрим двухфакторный случай. Тогда имеем ситуацию, описываемую формулой

Отсюда получаем:

где σ — это дисперсия соответствующего признака, отраженного в индексе.

МНК применим к уравнению МР в стандартизируемом масштабе. В таком случае получаем уравнение:

в котором t y , t x 1, … t xm — стандартизируемые переменные, для которых средние значения равны 0; β i — стандартизированные коэффициенты регрессии, а среднеквадратическое отклонение — 1.

Обратите внимание, что все β i в данном случае заданы, как нормируемые и централизируемые, поэтому их сравнение между собой считается корректным и допустимым. Кроме того, принято осуществлять отсев факторов, отбрасывая те из них, у которых наименьшие значения βi.

Задача с использованием уравнения линейной регрессии

Предположим, имеется таблица динамики цены конкретного товара N в течение последних 8 месяцев. Необходимо принять решение о целесообразности приобретения его партии по цене 1850 руб./т.

	номер месяца	название месяца	цена товара N
			1750 рублей за тонну
			1755 рублей за тонну
			1767 рублей за тонну
			1760 рублей за тонну
			1770 рублей за тонну
			1790 рублей за тонну
			1810 рублей за тонну
			1840 рублей за тонну

Для решения этой задачи в табличном процессоре «Эксель» требуется задействовать уже известный по представленному выше примеру инструмент «Анализ данных». Далее выбирают раздел «Регрессия» и задают параметры. Нужно помнить, что в поле «Входной интервал Y» должен вводиться диапазон значений для зависимой переменной (в данном случае цены на товар в конкретные месяцы года), а в «Входной интервал X» — для независимой (номер месяца). Подтверждаем действия нажатием «Ok». На новом листе (если так было указано) получаем данные для регрессии.

Строим по ним линейное уравнение вида y=ax+b, где в качестве параметров a и b выступают коэффициенты строки с наименованием номера месяца и коэффициенты и строки «Y-пересечение» из листа с результатами регрессионного анализа. Таким образом, линейное уравнение регрессии (УР) для задачи 3 записывается в виде:

Цена на товар N = 11,714* номер месяца + 1727,54.

или в алгебраических обозначениях

y = 11,714 x + 1727,54

Анализ результатов

Чтобы решить, адекватно ли полученное уравнения линейной регрессии, используются коэффициенты множественной корреляции (КМК) и детерминации, а также критерий Фишера и критерий Стьюдента. В таблице «Эксель» с результатами регрессии они выступают под названиями множественный R, R-квадрат, F-статистика и t-статистика соответственно.

КМК R дает возможность оценить тесноту вероятностной связи между независимой и зависимой переменными. Ее высокое значение свидетельствует о достаточно сильной связи между переменными «Номер месяца» и «Цена товара N в рублях за 1 тонну». Однако, характер этой связи остается неизвестным.

Квадрат коэффициента детерминации R 2 (RI) представляет собой числовую характеристику доли общего разброса и показывает, разброс какой части экспериментальных данных, т.е. значений зависимой переменной соответствует уравнению линейной регрессии. В рассматриваемой задаче эта величина равна 84,8%, т. е. статистические данные с высокой степенью точности описываются полученным УР.

F-статистика, называемая также критерием Фишера, используется для оценки значимости линейной зависимости, опровергая или подтверждая гипотезу о ее существовании.

(критерий Стьюдента) помогает оценивать значимость коэффициента при неизвестной либо свободного члена линейной зависимости. Если значение t-критерия > t кр, то гипотеза о незначимости свободного члена линейного уравнения отвергается.

В рассматриваемой задаче для свободного члена посредством инструментов «Эксель» было получено, что t=169,20903, а p=2,89Е-12, т. е. имеем нулевую вероятность того, что будет отвергнута верная гипотеза о незначимости свободного члена. Для коэффициента при неизвестной t=5,79405, а p=0,001158. Иными словами вероятность того, что будет отвергнута верная гипотеза о незначимости коэффициента при неизвестной, равна 0,12%.

Таким образом, можно утверждать, что полученное уравнение линейной регрессии адекватно.

Задача о целесообразности покупки пакета акций

Множественная регрессия в Excel выполняется с использованием все того же инструмента «Анализ данных». Рассмотрим конкретную прикладную задачу.

Руководство компания «NNN» должно принять решение о целесообразности покупки 20 % пакета акций АО «MMM». Стоимость пакета (СП) составляет 70 млн американских долларов. Специалистами «NNN» собраны данные об аналогичных сделках. Было принято решение оценивать стоимость пакета акций по таким параметрам, выраженным в миллионах американских долларов, как:

• кредиторская задолженность (VK);
• объем годового оборота (VO);
• дебиторская задолженность (VD);
• стоимость основных фондов (СОФ).

Кроме того, используется параметр задолженность предприятия по зарплате (V3 П) в тысячах американских долларов.

Решение средствами табличного процессора Excel

Прежде всего, необходимо составить таблицу исходных данных. Она имеет следующий вид:

• вызывают окно «Анализ данных»;
• выбирают раздел «Регрессия»;
• в окошко «Входной интервал Y» вводят диапазон значений зависимых переменных из столбца G;
• щелкают по иконке с красной стрелкой справа от окна «Входной интервал X» и выделяют на листе диапазон всех значений из столбцов B,C, D, F.

Отмечают пункт «Новый рабочий лист» и нажимают «Ok».

Получают анализ регрессии для данной задачи.

Изучение результатов и выводы

«Собираем» из округленных данных, представленных выше на листе табличного процессора Excel, уравнение регрессии:

СП = 0,103*СОФ + 0,541*VO - 0,031*VK +0,405*VD +0,691*VZP - 265,844.

В более привычном математическом виде его можно записать, как:

y = 0,103*x1 + 0,541*x2 - 0,031*x3 +0,405*x4 +0,691*x5 - 265,844

Данные для АО «MMM» представлены в таблице:

Подставив их в уравнение регрессии, получают цифру в 64,72 млн американских долларов. Это значит, что акции АО «MMM» не стоит приобретать, так как их стоимость в 70 млн американских долларов достаточно завышена.

Как видим, использование табличного процессора «Эксель» и уравнения регрессии позволило принять обоснованное решение относительно целесообразности вполне конкретной сделки.

Теперь вы знаете, что такое регрессия. Примеры в Excel, рассмотренные выше, помогут вам в решение практических задач из области эконометрики.